Database Math – Page 3 – Database mathematics and more pragmatic information.

MSSQL Server: Opening the Required Firewall Ports

Firewalls are obviously a very important and fundamental part of network security. However, that doesn’t make them any less annoying when you’re working in development or just trying to learn the nitty gritty. You may be tempted to just disable the firewall. This will work and you’ll be on your merry way but you’ve learned nothing and when its time to deploy it can be a headache.

When it comes to Microsoft SQL Server, the default instance is easy enough. It operates on port 1433 out-of-the-box. Lets look at how to open this port a couple of different ways.

Using the GUI

To open it up for remote access, simply open Windows Defender Firewall -> Advanced Settings -> Inbound Rules -> New Rule… then follow the wizard:

Select Port and click Next.

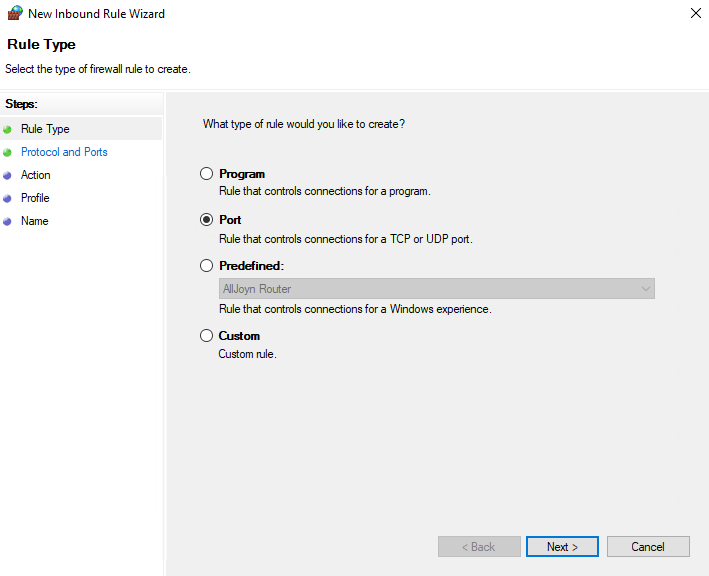
Select TCP and type 1433 into the Specify local ports field

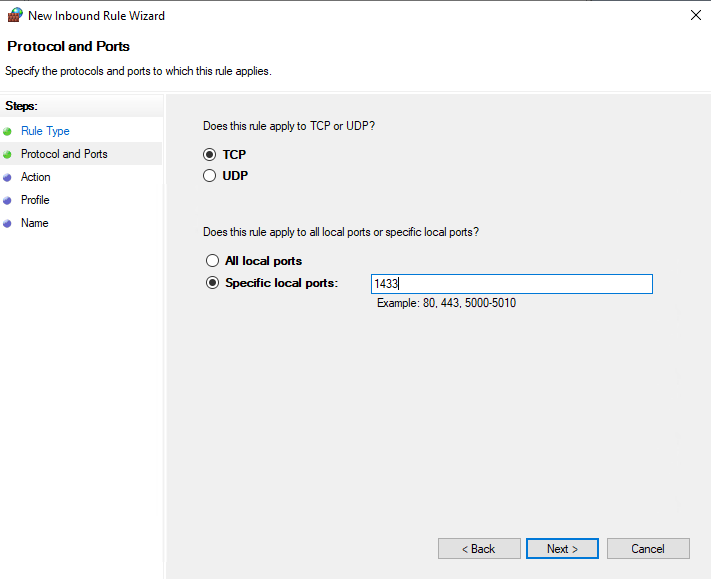
New Inbound Rule Wizard: Protocol and Ports

Select Allow the connection and click Next.

Select the Network Profiles that you want the rules to apply to.

Give the rule a name and description the click Finish.

Using netsh advfirewall

Using the GUI can be time consuming, if you have multiple machines were you need to open ports we can use the netsh utility to administer the firewall through the command line or a batch file.

Running this command will create an inbound rule that opens communication on port 1433 for the domain network profile:

netsh advfirewall firewall add rule name = SQLPort dir = in protocol = tcp action = allow localport = 1433 remoteip = localsubnet profile = DOMAIN

By default, the typical ports used by SQL Server and associated database engine services are: TCP 1433, 4022, 135, 1434, UDP 1434. The table below explains these ports in greater detail. A named instance uses dynamic ports.

The following table lists the ports that are frequently used by the Database Engine.

Scenario	Port	Comments
Default instance running over TCP	TCP port 1433	This is the most common port allowed through the firewall. It applies to routine connections to the default installation of the Database Engine, or a named instance that is the only instance running on the computer. (Named instances have special considerations. See Dynamic Ports later in this article.)
Named instances with default port	The TCP port is a dynamic port determined at the time the Database Engine starts.	See the discussion below in the section Dynamic Ports. UDP port 1434 might be required for the SQL Server Browser Service when you are using named instances.
Named instances with fixed port	The port number configured by the administrator.	See the discussion below in the section Dynamic Ports.
Dedicated Admin Connection	TCP port 1434 for the default instance. Other ports are used for named instances. Check the error log for the port number.	By default, remote connections to the Dedicated Administrator Connection (DAC) are not enabled. To enable remote DAC, use the Surface Area Configuration facet. For more information, see Surface Area Configuration.
SQL Server Browser service	UDP port 1434	The SQL Server Browser service listens for incoming connections to a named instance and provides the client the TCP port number that corresponds to that named instance. Normally the SQL Server Browser service is started whenever named instances of the Database Engine are used. The SQL Server Browser service does not have to be started if the client is configured to connect to the specific port of the named instance.
Instance with HTTP endpoint.	Can be specified when an HTTP endpoint is created. The default is TCP port 80 for CLEAR_PORT traffic and 443 for SSL_PORT traffic.	Used for an HTTP connection through a URL.
Default instance with HTTPS endpoint	TCP port 443	Used for an HTTPS connection through a URL. HTTPS is an HTTP connection that uses Transport Layer Security (TLS), previously known as Secure Sockets Layer (SSL).
Service Broker	TCP port 4022.	There is no default port for SQL ServerService Broker, but this is the conventional configuration used in Books Online examples.
Database Mirroring	Administrator chosen port.	There is no default port for database mirroring however Books Online examples use TCP port 5022 or 7022. It is important to avoid interrupting an in-use mirroring endpoint, especially in high-safety mode with automatic failover. Your firewall configuration must avoid breaking quorum. For more information, see Specify a Server Network Address (Database Mirroring).
Replication	Replication connections to SQL Server use the typical regular Database Engine ports (TCP port 1433 for the default instance, etc.) Web synchronization and FTP/UNC access for replication snapshot require additional ports to be opened on the firewall. To transfer initial data and schema from one location to another, replication can use FTP (TCP port 21), or sync over HTTP (TCP port 80) or File Sharing. File sharing uses UDP port 137 and 138, and TCP port 139 if it using NetBIOS. File Sharing uses TCP port 445.	For sync over HTTP, replication uses the IIS endpoint (ports for which are configurable but is port 80 by default), but the IIS process connects to the backend SQL Server through the standard ports (1433 for the default instance. During Web synchronization using FTP, the FTP transfer is between IIS and the SQL Server publisher, not between subscriber and IIS.
Transact-SQL debugger	TCP port 135 See Special Considerations for Port 135 The IPsec exception might also be required.	If using Visual Studio, on the Visual Studio host computer, you must also add Devenv.exe to the Exceptions list and open TCP port 135. If using Management Studio, on the Management Studio host computer, you must also add ssms.exe to the Exceptions list and open TCP port 135.

Service Broker and AlwaysOnAG (mirroring) don’t have defaults. If you need to check what these ports are configured as on an existing system, connect via SSMS or SQLCMD and run the following queries:

AlwaysOn AG (Mirroring):

SELECT name, protocol_desc, port, state_desc 
   FROM sys.tcp_endpoints
   WHERE type_desc = 'DATABASE_MIRRORING'

Service Broker:

SELECT name, protocol_desc, port, state_desc
   FROM sys.tcp_endpoints
   WHERE type_desc = 'SERVICE_BROKER'

Batch Script

Below is an example batch script that creates all of the aforementioned firewall rules. Modify the ag_endpnt and sb_endpnt variable at the beginning if your ports are different. Script should be executed from an elevated command prompt or powershell window. Provided for educational purposes only and as always don’t run anything in production that you haven’t tested first.

rem OpenSQLServerPorts.bat
rem Date Modified: 03/26/2021
rem Author: Avery Lane

set "ag_endpnt=5022"
set "sb_endpnt=4022"

rem SQL Default Ports Inbound/Outbound
netsh advfirewall firewall add rule name = SQLPort dir = in protocol = tcp action = allow localport = 1433 remoteip = localsubnet profile = DOMAIN
netsh advfirewall firewall add rule name = SQLPort dir = out protocol = tcp action = allow localport = 1433 remoteip = localsubnet profile = DOMAIN

rem SQL Dedicated Admin Port Inbound (Default Instance)
netsh advfirewall firewall add rule name = SQLPortDedicatedAdmin dir = in protocol = tcp action = allow localport = 1434 remoteip = localsubnet profile = DOMAIN

rem SQL Database mirroring/AlwaysOn AG (Default is 5022)
netsh advfirewall firewall add rule name = SQLPortAG dir = in protocol = tcp action = allow localport ="%ag_endpnt%" remoteip = localsubnet profile = DOMAIN
netsh advfirewall firewall add rule name = SQLPortAG dir = out protocol = tcp action = allow localport ="%ag_endpnt%" remoteip = localsubnet profile = DOMAIN

rem SQL Browser Service
netsh advfirewall firewall add rule name = SQLPortBrowser dir = in protocol = udp action = allow localport = 1434 remoteip = localsubnet profile = DOMAIN

rem Service Broker (Default is 4022)
netsh advfirewall firewall add rule name = SQLPortServiceBroker dir = in protocol = tcp action = allow localport ="%sb_endpnt%" remoteip = localsubnet profile = DOMAIN
netsh advfirewall firewall add rule name = SQLPortServiceBroker dir = out protocol = tcp action = allow localport = "%sb_endpnt%" remoteip = localsubnet profile = DOMAIN

rem Replication
netsh advfirewall firewall add rule name = SQLReplUDP dir = in protocol = udp action = allow localport = 137,138 remoteip = localsubnet profile = DOMAIN
netsh advfirewall firewall add rule name = SQLReplTCP dir = in protocol = tcp action = allow localport = 139,445 remoteip = localsubnet profile = DOMAIN

netsh advfirewall firewall add rule name = SQLReplUDP dir = out protocol = udp action = allow localport = 137,138 remoteip = localsubnet profile = DOMAIN
netsh advfirewall firewall add rule name = SQLReplTCP dir = out protocol = tcp action = allow localport = 139,445 remoteip = localsubnet profile = DOMAIN

Output of netsh advfirewall firewall add rule ?

Usage:
      add rule name=<string>
      dir=in|out
      action=allow|block|bypass
      [program=<program path>]
      [service=<service short name>|any]
      [description=<string>]
      [enable=yes|no (default=yes)]
      [profile=public|private|domain|any[,...]]
      [localip=any|<IPv4 address>|<IPv6 address>|<subnet>|<range>|<list>]
      [remoteip=any|localsubnet|dns|dhcp|wins|defaultgateway|
         <IPv4 address>|<IPv6 address>|<subnet>|<range>|<list>]
      [localport=0-65535|<port range>[,...]|RPC|RPC-EPMap|IPHTTPS|any (default=any)]
      [remoteport=0-65535|<port range>[,...]|any (default=any)]
      [protocol=0-255|icmpv4|icmpv6|icmpv4:type,code|icmpv6:type,code|
         tcp|udp|any (default=any)]
      [interfacetype=wireless|lan|ras|any]
      [rmtcomputergrp=<SDDL string>]
      [rmtusrgrp=<SDDL string>]
      [edge=yes|deferapp|deferuser|no (default=no)]
      [security=authenticate|authenc|authdynenc|authnoencap|notrequired
         (default=notrequired)]

Remarks:

      - Add a new inbound or outbound rule to the firewall policy.
      - Rule name should be unique and cannot be "all".
      - If a remote computer or user group is specified, security must be
        authenticate, authenc, authdynenc, or authnoencap.
      - Setting security to authdynenc allows systems to dynamically
        negotiate the use of encryption for traffic that matches
        a given Windows Defender Firewall rule. Encryption is negotiated based on
        existing connection security rule properties. This option
        enables the ability of a machine to accept the first TCP
        or UDP packet of an inbound IPsec connection as long as
        it is secured, but not encrypted, using IPsec.
        Once the first packet is processed, the server will
        re-negotiate the connection and upgrade it so that
        all subsequent communications are fully encrypted.
      - If action=bypass, the remote computer group must be specified when dir=in.
      - If service=any, the rule applies only to services.
      - ICMP type or code can be "any".
      - Edge can only be specified for inbound rules.
      - AuthEnc and authnoencap cannot be used together.
      - Authdynenc is valid only when dir=in.
      - When authnoencap is set, the security=authenticate option becomes an
        optional parameter.

Reference Links & More Information

BASE and CAP

BASE Model

NoSQL (actually short for “not only” SQL) often times rely on a softer transaction model than ACID abbreviated as BASE:

Basically Available
Soft State
Eventually Consistent

Basically Available

This has to do with the perceived availability of the data. The idea is for data to always be available even if it is not in a consistent or hardened state. There are no isolation levels. One transaction may access a file that is being actively modified by another.

Soft State

Values stored in the database may change because of the eventual consistency model.

Eventually Consistent

Data and changes to said data are replicated across nodes and eventually become consistent. For example, in Hadoop, when a file is written to the HDFS, the replicas of the data blocks are created in different data nodes after the original data blocks have been written. For the short period before the blocks are replicated, the state of the file system isn’t consistent.

As tongue in cheek as BASE is, it’s a bit misleading. It is not meant to be the polar opposite of ACID because most NoSQL implementations do not abandon all ACID principles. Soft State and Eventually Consistent are also so closely related that their distinction serves no real purpose.

The point though, is that a BASE model uses a more relaxed approach to consistency for the sake of being able to scale horizontally much more easily and provide a high degree of availability.

This model is very popular with social media platforms and search engines where “some (maybe partial) results now” is much more important than “all results no matter how long it takes”.

CAP Theorem

Also known as Brewer’s theorem, named after computer scientist Eric Brewer, proposes that it is only possible for a distributed data store to provide two out of the three following guarantees:

Consistency: Every read receives the most recent write or an error

Availability: Every request receives a (non-error) response, without the guarantee that it contains the most recent write

Partition tolerance: The system continues to operate despite an arbitrary number of messages being dropped (or delayed) by the network between nodes

Transactions and ACID

A database transaction is a unit of work performed against a database that is independent of other transactions. The purpose of a transaction is two-fold:

To provide a reliable record and means to recover in case of failure when performing work.
To provide isolation between applications or processes that are accessing data concurrently.

In any good relational database management system, transactions adhere to a set of strict rules or properties abbreviated as ACID:

Atomicity
Consistency
Isolation
Durability

Atomicity

Guarantees that either all operations in the transaction succeed or they all fail. This prevents partial updates that could leave a database in a questionable or incomplete state. For instance, imagine your database transaction was a financial transaction that transferred money from one account to another. That would consist of two operations: a deduction from account A and a deposit into account B. This is an obvious example where we want both operations to succeed or both to fail. If only one operation was successful we would either be destroying money or inventing new money from nothing (something apparently only the federal reserve is allowed to do).

Consistency

Is similar to atomicity but has more to do with referential integrity. This is where constraints come into play, such as a primary key. If you have an ID column used to track rows based on a unique identifier, you wouldn’t want to allow multiple rows to have the same value for ID; if there were the database would be in an inconsistent state. A transaction that preserves consistency ensures that the database is in a consistent state when the transaction begins and when the transaction ends.

Isolation

This protects transactions from the effects of other transactions via mechanisms like locks and row versioning. Database management systems typically employ different levels of isolation. For instance, in Microsoft SQL Server, the READ UNCOMMITTED isolation level allows transactions to read data that other transactions are modifying, while the stricter SERIALIZABLE isolation level will lock ranges of rows or entire tables to prevent the reading of data until the transaction modifying data completes and commits.

Durability

A transaction is considered durable when it commits and stays committed. This is accomplished by flushing the data to a stable/nonvolatile media (think disk vs in-memory) although as storage mediums continue to advance and innovate, the implementation may change. The important thing is that the work is saved and is not prone to being lost or rolled back without intervention.

Microsoft SQL Server, Oracle, MySQL, and PostgreSQL are some of the most popular database systems which follow ACID properties by default.

Logic: An Introduction (Part III)

Truth Tables

As discussed in the previous post, compound predicates are built from other predicates and propositions using logical connectives (¬, ∧, ∨, ⇒, ↔). The truth value of the compound predicate depends on the truth values of its components.

Truth tables can be used to define the meaning of logical operators and to investigate compound expressions. By investigating the truth values of compound expressions, you can establish new logical concepts. This is especially useful when it comes to rewrite rules which we will discuss a little bit later on.

Components of a Truth Table

Truth tables consists of a header and a body. When defining the meaning of a logical connective, the leftmost column lists the variable you are evaluating and the rightmost column lists the connective.

Example:

This truth table defines the conjunction connective. By looking at this truth table we can see that if P and Q both have a truth value of TRUE then the expression P ∧ Q also has a truth value of TRUE, but any other combination of P and Q means that the truth value of P ∧ Q is FALSE.

Variables
Logical
Expression
PAQ
Header
Body

When investigating the truth value for a compound expression, the left most column headers list the variables and the rightmost header lists the compound expression.

The Body of a truth table always contains one row for every possible combination of the variables involved.

Note: The variables in a truth table are propositional variables. This allows you to work with the most simplified form of possible combinations and outcomes.

Here are truth tables for all of the logical connectives:

Negation
Con•unction
Implication
E uivalence
Disjunction

Note: Regarding the truth table for the Disjunction connective, this table shows the truth values for what is referred to as the inclusive or. This means that the proposition evaluates to TRUE if P and Q are both TRUE. You may encounter times when the exclusive or is specified (sometimes called XOR or EOR). This simply means that one of the criterion must be true but not both.

Equivalence and Implication

These two connectives may not be as immediately apparent or intuitive and the others so I think they warrant a bit more discussion.

Equivalence

This one isn’t too bad. It’s basically the same as the = operator (Note to self: check thesaurus for “same as”). It evaluates to TRUE if and only if the two involved propositional variables evaluate to the same truth value (either both TRUE or both FALSE).

Implication

This one is a bit more confusing because of the way “implies” is used informally versus its mathematical logical meaning. To better explain what the Implication connective means, I think it would be easier to start with what it doesn’t mean:

It doesn’t mean “suggests”.
It doesn’t mean “causes”.

The following sentence is completely logical under the mathematical definition of Implication:

“The sky is blue implies January is a month”

This does not mean “Since the sky is blue January is a month” or “January is a month because the sky is blue”

Note: Always remember that the ONLY time that an implies statement is FALSE is if the Antecedent (P) is TRUE but the Consequent (Q) is FALSE.

So let’s take a closer look at the Implication truth table again:

To better understand this, it might be better to evaluate the conditions in stages. We will start by examining the truth values for P. If the truth value for P is FALSE, we aren’t even going to check what the truth value for Q is because we already know that the expression is TRUE. If P is TRUE then we have to go on to evaluate if Q is TRUE, if it is the expression is TRUE, but if it isn’t then the expression is FALSE.

I like to think of this as “Innocent until proven guilty” or “True until proven false”.

Example:

Proposition: If your pet is a dog, then your pet is a male.

Suppose my pet is a dog… ok now I can check the gender… it turns out my dog is male… the statement must be true

Suppose my pet is a dog… ok now I can check the gender… it turns out my dog is female… I’ve proven the statement false

Suppose my pet is a cat… ok I could check the gender but it doesn’t really matter because the statement only applies to dogs so I wouldn’t be proving anything even if my cat was female… without evidence to prove that the statement wrong, I must assume that it is true.

Suppose my pet is a bird… same logic applies as if my pet was a cat… without evidence to prove that the statement wrong, I must assume that it is true.

Implication is probably the least intuitive of all the connectives and some of that probably comes from how we think about “implications” outside of mathematics. Let’s consider for a moment why this is.

Consider the following scenario:

I have a bag of 10 marbles. One is blue and nine are yellow.

I ask you to pick one marble out of the bag without looking and offer the following implication:

“If you pick a blue marble, the next will be yellow”

So you pick a marble:

Suppose I pick a blue marble… ok now I can pick another marble… it turns out it is yellow… The statement must be true. (T ⇒ T) = T

Suppose I pick a blue marble… ok now I can pick another marble… it turns out it is blue… The statement must be false. (T ⇒ F) = F

Those two seem pretty intuitive right? So let’s look at the tricky ones:

Suppose I pick a yellow marble… ok now I can pick another marble… it turns out it is also a yellow marble… ok so I don’t have enough information to know if the original statement is true or not. In real life if a friend asked me to do this and draw a conclusion I would say that there isn’t enough information to determine if it is TRUE or FALSE because the first marble I drew wasn’t blue so can’t actually test the hypothesis. Ahhh but let’s remember our definition of a proposition: a declarative sentence that when evaluated is either TRUE or FALSE, but not both.

By definition, our implication proposition MUST evaluate to either TRUE or FALSE, it cannot be both or neither. So now the question really becomes given this scenario, do we assume FALSE or do we assume TRUE? When it comes to implication, we always assume TRUE. This is why I use the phrase “innocent until proven guilty”. Just like in a court of law, the defendant is innocent until they can be proven guilty. Likewise when it comes to an implication, we assume that the overall statement (P ⇒ Q) is TRUE unless we can definitively prove that it is FALSE.

Predicate Strength

You can think about Implication as “ordering” the predicates that make up its operands. This order is referred to as the strength of the predicate. The “strongest” predicate is the one that implies the other. Consider P ⇒ Q, in this situation P is the stronger predicate and Q is the weaker.

Example:

The variable x is defined with a type of integer.

Consider the predicate: x > 5 ⇒ x > 0

To state that x is greater than 5 implies that x is greater than 0. This implication is TRUE regardless of the value of x, and the predicate x > 5 is the stronger predicate while x > 0 is the weaker one.

The only time that both predicates are of equal strength is when P ⇒ Q and Q ⇒ P. When the predicates are of equal strength they are equivalent: ↔

Logic: An Introduction (Part II)

Logical Connectives

In my last blog post we discussed propositions and predicates. To summarize, a proposition is a declarative sentence that can be proven TRUE or FALSE. Similarly, a predicate takes the form of a declarative sentence but contains at least one embedded variable (parameter) and cannot be evaluated as TRUE or FALSE unless input for said parameters is provided.

A logical connective is an operator that is used to form more complex predicates by combining predicates together. The most well-known of these logical connectives are conjunction (logical AND), disjunction (logical OR), and negation (logical NOT). Probably less commonly known are implication and equivalence.

Symbol	Meaning	Terminology
¬	NOT	Negation
∧	AND	Conjunction
∨	OR	Disjunction
⇒	IMPLIES	Implication (if…then…)
↔	IS EQUIVALENT TO	Equivalence (if and only if)

Note: If you take a course in mathematical logic, you will have a formal discussion of proofs. You start with a formal language, which describes the symbols you're allowed to use and how to combine them, and the rules of inference, which describe the valid ways of making steps in a proof. This is important because natural languages like English are informal and imprecise, as a consequence, the meaning of words sometimes depends on context; this kind of ambiguity is why formal language and symbols exist. However, throughout my writings I will use a mix of formal and informal language and syntax for the sake of learning.

Simple and Compound Predicates

If a logical connective is regarded as a logical operator, we can say that it takes one or more predicates as its operand and returns another predicate.

Example:

Consider the logical operator ∧

Consider the predicates x = 11 and y = 15 as the operands

The compound predicate would be (x = 11) ∧ (y = 15)

In informal language this reads as: I propose that x equals 11 and y equals 15.

With an AND operator, the compound predicate only evaluates to TRUE if both the simple predicates also individually evaluate to TRUE.

Note: The simple predicates that make up the operands of the logical operator are also sometimes referred to as components of the compound predicate. Isn’t natural language fun?

Propositional Variables

Let’s consider another kind of compound predicate. Consider the following:

P ∧ Q ⇒ P ⇒ Q

This looks a bit different than the predicates we’ve looked at so far. That’s because this example uses the propositional variables P and Q. If you consider that a variable is a “holder” for a value, then you can think of a propositional variable as a “holder” for a proposition.

An assertion that contains at least one propositional variable is referred to as a propositional form. If you substitute all propositional variables (of the given propositional form) with a proposition the propositional form is transformed into a proposition in and of itself.

Phew, even reading that back to myself that is a tricky sentence. You may think at this point that a propositional form seems very similar to a predicate. So what’s the difference? Well, let’s recall that a predicate takes the form of a declarative sentence (just like a proposition) but has embedded variables. A predicate cannot be evaluated to TRUE or FALSE until values are substituted for these variables. Meanwhile a propositional form uses propositional variables which themselves represent a truth value (TRUE or FALSE).

This means that we can treat propositional variables as arbitrary predicates with truth values without having to fully express the details of the underlying proposition

Example:

Let P represent 3 + 5 = 8

Let Q represent 1 + 1 = 2

Consider the propositional form P ∧ Q

If we replace the proposition variables (P,Q) the propositional form is transformed to the following proposition:

3 + 5 = 8 ∧ 1 +1 = 2

Which evaluates to TRUE.

Similarly, we can use letters like P,Q,R, ect. In expressions like this:

P(x), Q(y), R(s,t)

These represent arbitrary predicates with parameters.

Example:

Let P represent 3 + 2x = 9

What is the value of P(x) given that x = 3

You would evaluate this by substituting P(3) which means to pass 3 as the value for parameter x to the predicate 3 + 2x = 9 which forms the proposition 3 + (2*3) = 9 which evaluates to TRUE and thus P(x) evaluates to TRUE

If we pass any other value for x, the resulting proposition evaluates to FALSE.

Logical Operator Precedence and Parentheses

I’m sure everyone remembers PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction), the order of operations from your middle school math class. Just like algebraic expressions follow the order of operations, logical expressions follow an order of precedence. And just like the algebraic expressions, you can override this order using parentheses.

Note: Even though formal rules of the syntax do not always strictly require parentheses, it is a good idea to add them even if redundant to avoid any confusion or misinterpretation. It increases readability and is just as valid.

Here are the Logical Connective Precedence Rules:

Rank	Connective
1	¬
2	∧, ∨
3	⇒, ↔

Note that some operators have the same rank.

Example:

Given P ∧ Q ⇒ R the precedence rules state that this is equivalent to (P ∧ Q) ⇒ R rather than P ∧ (Q ⇒ R)

For operations with equal rank, formal rules state that you should read operations from right to left. This is called the associative rule.

Example:

Given P ⇒ Q ⇒ R, the associative rule states that this should be equivalent to P ⇒ (Q ⇒ R) rather than (P ⇒ Q) ⇒ R

This is an important rule to keep in mind, but for the sake of clarity I will most often use parentheses in my posts.

Logic: An Introduction (Part I)

Values, Variables and Types

Regardless of your background, you probably have at least some idea about what the terms values and variables mean. However, when talking about them in a technical context it is important to be precise as they are often used interchangeably when they ought not be.

A value is an individual constant which is well-defined. Being a constant means that it is fixed and well-defined means that it is unambiguous. For example, the integer 42 is a value (and the answer to the ultimate question of life, the universe, and everything). You cannot update or change a value because if you did it would no longer be the same value. A value can be represented in many different ways (through encoding) but it always represents the same thing.

A variable is a holder or a container for a value. As such the value of a variable is not fixed. Or put another way, which value the variable is holding can change. Variables have a name, which can be used to reference them without the requirement of knowing what value (or set of values) it contains. Given x = 1 + 3 as an example, x is a variable and it holds the value 4 which is the result of the operation (1+3).

A variable’s type is the entire set or range of values that a variable is allowed to hold.

Propositions and Predicates

In logic, the primary components we will deal with are propositions and predicates.

A proposition (also sometimes referred to as a statement) is a declarative sentence that when evaluated is either TRUE or FALSE, but not both.

Example:

In English, the sentence “The sky is beautiful” is NOT a proposition because while it does make an assertion, it is a subjective one since it is a matter of opinion. Some would evaluate the this assertion as TRUE while others would deem it FALSE. Thus it is ambiguous and thus not a proposition.

The sentence “Is it raining?” is not a proposition because it is a question rather than an assertion or a declaration.

The sentence “Right now, it is 5:00PM Pacific Time in Seattle, Washington” is a proposition because it makes a well-defined assertion which either is or is not.

Some sentences that are mathematical in nature often are not statements because we may not know precisely what a variable represents.

Example:

Consider the equation (2x)+5 = 15. This is NOT a proposition because we do not know what the variable represents. Remember that in order for something to be a proposition it must be either true or false but not both.

Consider the equation 4 + 1 = 5. This is a proposition because without any additional information we can evaluate this as either TRUE or FALSE. In this case it is TRUE.

Note: It is a common mistake to only consider TRUE sentences as valid propositions but propositions can also be FALSE; the important consideration when defining a proposition is that it cannot be both.

A predicate is something which has the form of a declarative sentence but which includes at least one embedded variable whose value is unknown and which you cannot determine to be TRUE or FALSE without knowing the value of said variable(s). We will refer to these embedded variables as the parameters of the predicate.

Example:

Using the same example as from above, the equation (2x)+5 = 15 is a predicate because without additional information, we don’t know what the value of x is and so we cannot determine if it is TRUE or not.

A predicate with n parameters is referred to as an n-place predicate. If you substitute one of the parameters in an n-place predicate with a value, it becomes an (n-1)-place predicate.

Example:

Consider the equation x + y = 5

This is a 2-place predicate; it has two parameters x and y.

Now, consider the same equation with the variable x substituted with the value 4:

4+ y = 5

This is a 1-place predicate; it has one parameter y.

So you may be wondering, if n = 1, wouldn’t an (n-1)-place predicate be a 0-place predicate? The answer is yes. Given the same equation from the previous example, if we replace the last remaining parameter y with a literal value such as 1, the equation becomes:

4 + 1 = 5

You may have noticed that this is the exact same equation as the example given for a proposition. That’s because a 0-place predicate is a proposition. In this way, a proposition can be thought of as a special case of predicates. You can transform a predicate into a proposition by replacing all of its parameters with values. This process is called instantiating the predicate with the given values.

The parameters of a predicate are also referred to as the free variables of a predicate. There is another way to convert predicates into propositions; binding them to a quantifier. Free variables then turn into what are referred to as bound variables. This process is called Quantification (over a set) and it is an important concept in logic and an especially important when it comes to data management.

Bonus:

Consider the following two sentences:

This statement is false.

I’m lying.

These are both self-referential sentences; meaning that they tell us something about themselves. Sentences like these have the potential to cause logical contradictions. The second sentence is called the Liar’s paradox. If you begin an evaluation of the sentence with the assumption that it is TRUE, you will reach the conclusion that it is in fact FALSE. However, if you begin an evaluation of the sentence with the assumption that it is FALSE, you will come to the conclusion that it is in fact TRUE. Because of this you are unable to determine if the sentence is TRUE or FALSE, despite the fact that there are no variables or parameters. The solution is to disregard the statement as a valid proposition.

Similarly, you must discard “ill-formed” expressions as predicates.

Consider the following:

2 is an element of 7

This is an ill-formed predicate because 7 is not a set, it is a value. The expression just doesn’t make any sense and so it should be disregarded. This assumes at least a familiarity with the concept of sets, but I’ll be covering basic set theory in a future post.